一、一元二次方程求最小值与最大值的公式是哪个
一般来说,如果这个一元二次函数的定义域是R的话：
（1）函数开口向上,即a>0时,则没有最大值,只有最小值,即函数的顶点,可用函数的顶点公式：(-b/2a,(4ac-b^2)/4a)来求.
（2）函数开口向上,即a<0时,则没有最小值,只有最大值,求法同上.
若该函数的定义域不是R的话：
（1）函数开口向上,即a>0时：
①当-b/2a在定义域内时,有最小值,再看定义域区间
假设是闭区间[m,n],若-b/2a>(n+m)/2,则最大值是x=m时的函数值,若-b/2a<(n+m)/2,则相反,若两者相同,则最大值即是端点值.
当定义域区间是开区间（m,n）时,则无最大值
还有就是区间是半开半闭的情况时,即[m,n)或(m,n]时,按上面闭区间的方法计算,但若x取不到,则没有最大值
②当-b/2a不在定义域内时,
假设是闭区间[m,n],则最小值和最小值就是两个端点值,算一下再比较大小就行
当定义域区间是开区间（m,n）时,则无最大最小值
当区间是半开半闭的情况,即[m,n)或(m,n]时,按上面闭区间的方法计算,关键是看能不能取到,但肯定是只有一个最值的
至于函数开口向下,即a<0的情况,上面的看懂了就会了
其实最方便的还是画个草图,分情况讨论一下就行了 ,算二次函数的最值问题只要不弄错定义域,情况分清楚,不讨论错还是很简单的
很高兴为你解答有用请采纳
二、一元二次方程函数最大最小值的公式什么
一元二次方程函数最大最小值的公式什么
不能这样说，只有二次函数才有最大值或最小值
二次函数的表达式一般是这样的：y=ax²+bx+c,这里如果y=0时上式便成为一元二次方程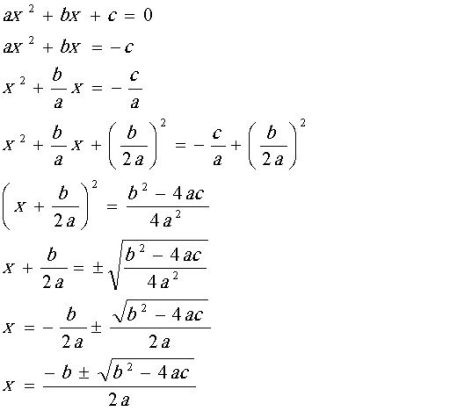
若y不等于零时则y=ax²+bx+c为二次函数。现在讨论二次函数的最大值和最小值
设二次函数为：y=ax²+bx+c
=a（x²+b/ax+ c/ a）
= a（x²+b/ax+ （b/2a）² -（b/2a）²+c/ a）
= a[（x+b/2a）²+（4 a c- b²）/4 a²]
如果x+b/2a=0时，则y有最大值或最小值；如果a〉0时则y有极大值，y=（4 a c- b²）/4 a² 如果a〈0时，则y有极小值（4 a c- b²）/4 a²。
三、一元二次方程怎么求最小值或者最大值
对于一元二次函数y=ax²+bx+c（a≠0）来说：
当 x=-b/2a 时，有最值；且最值公式为：（4ac—b^2）/4a
当a>0时， 为最小值， 当a<0时， 为最大值。
扩展资料：
一元二次方程经过整理都可化成一般形式ax²+bx+c=0（a≠0）。其中ax²叫作二次项，a是二次项系数；bx叫作一次项，b是一次项系数；c叫作常数项。
成立条件
一元二次方程成立必须同时满足三个条件：
1、是整式方程，即等号两边都是整式，方程中如果有分母；且未知数在分母上，那么这个方程就是分式方程，不是一元二次方程，方程中如果有根号，且未知数在根号内，那么这个方程也不是一元二次方程（是无理方程）。
2、只含有一个未知数；
3、未知数项的最高次数是2
参考资料来源：百度百科-一元二次方程
四、如何用1元2次方程求最小值和最大值？
首先看二次项系数是正是负，如果是正数的话，说明曲线开口向上，然后求X=-b/(2a)，再求出Y值就是该去方程的最小值。如果二次项系数为负数的话，对应求出的Y值就是方程的最大值。
只含有一个未知数（一元），并且未知数项的最高次数是2（二次）的整式方程叫做一元二次方程。一元二次方程经过整理都可化成一般形式ax²+bx+c=0（a≠0）。其中ax²叫作二次项，a是二次项系数；bx叫作一次项，b是一次项系数；c叫作常数项。
一元二次方程成立必须同时满足三个条件：
1、是整式方程，即等号两边都是整式，方程中如果有分母；且未知数在分母上，那么这个方程就是分式方程，不是一元二次方程，方程中如果有根号，且未知数在根号内，那么这个方程也不是一元二次方程（是无理方程）。
2、只含有一个未知数；
3、未知数项的最高次数是2。
扩展资料：
一元二次方程解法：
一、直接开平方法
形如（x+a)^2=b，当b大于或等于0时，x+a=正负根号b，x=-a加减根号b；当b小于0时。方程无实数根。
二、配方法
1、二次项系数化为1
2、移项，左边为二次项和一次项，右边为常数项。
3、配方，两边都加上一次项系数一半的平方，化成（x=a)^2=b的形式。
4、利用直接开平方法求出方程的解。
三、公式法
现将方程整理成：ax^2+bx+c=0的一般形式。再将abc代入公式x=(-b±√(b^2-4ac))/2a，(b^2-4ac大于或等于0）即可。
四、因式分解法
如果一元二次方程ax^2+bx+c=0中等号左边的代数式容易分解，那么优先选用因式分解法。
