一、大小于号怎么区分
可以根据符号的“口”朝向区分大于号和小于号:开口朝左的“>”就是大于号,开口朝右的“<”就是小于号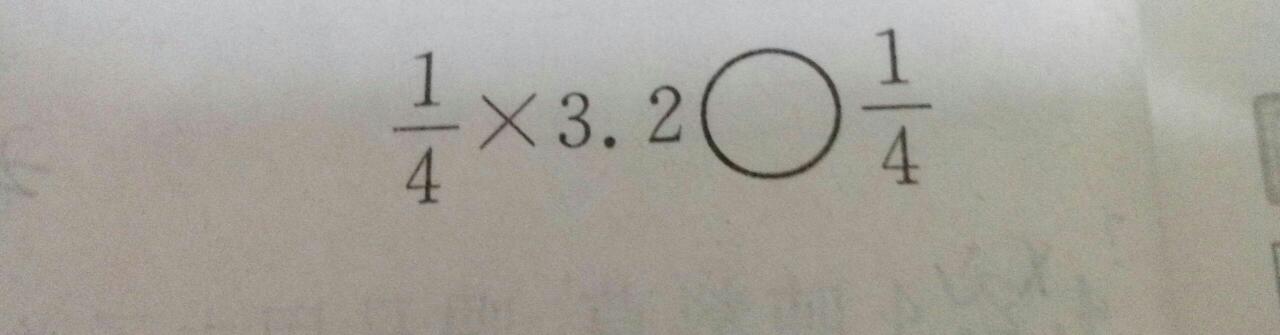
大于号左边的大于右边的,小于号左边的小于右边的。
例如5>3,表示左边的5大于右边的3;3<5表示左边的3小于右边的5。
扩展资料:
大小于号的发明
大小于号是英国数学家哈利奥特1631年开始采用,而他本人使用大于号、小于号的符号则因应于1631年。托马斯·哈里奥特Thomas Harriot(1560年 –1621年),是英国著名的天文学家,数学家,翻译家。他于1621年7月2日去世于伦敦。
在他的《使用分析学》(Artis Analyticae Praxis)一书中首先使用了“<”和“>”符号,但是直到他去世十年之后1631年才发表。所以一般认为是1631年才开始使用。现今通用之大于号“>”及小于号“<”,但并未被当时数学界所接受,直至百多年后才渐成标准之应用符号。
庞加莱与波莱尔于1901年引入符号<<(远小于)和>>(远大于),很快为数学界所接受,沿用至今。
二、大小于号怎么区分?
区分方法:
区分“>”与“<”,开口朝左的就是大于号,另一个就是小于号。
区分大于号和小于号的口诀:
左边大,大于号;左边小,小于号。
大于号开口在左边,小于号开口在右边。
开口旁边是大数,尖尖旁边是小数。
开口朝大数,尖尖朝小数。
扩展资料:
大于号小于号的来历:
英国数学家哈利奥特在自己的《使用分析学》一书中首先使用了“<”和“>”符号,但是直到他去世十年之后1631年才发表。a 大于等于的数学符号为≥。当一个数值比另一个数值大或两数相等时使用大于等于号"≥",又被称为“不小于”。对于任意两实数a,b,都可在同一数轴上找到其对应点A,B。若点A在点B右侧或A与B重合,则a≥b。 小于等于是一种判断方式,用来表示不等式左侧的值小于等于不等式右侧的值,符号为“≤”。 庞加莱与波莱尔于1901年引入符号<<(远小于)和>>(远大于),很快为数学界所接受,沿用至今。 参考资料:百度百科-大于 参考资料:百度百科-小于 大于号和小于号区分具体如下: 1、开口方向不同:大于号开口方向是这样的>,小于号开口方向是这样的<。 2、二者名字不同:大于号的名字是大于号,小于号的名字是小于号。 3、二者表示含义含义不同:大于号左边的大于右边的,小于号左边的小于右边的。大于等于的数学符号为≥。当一个数值比另一个数值大或两数相等时使用大于等于号"≥",又被称为“不小于”。对于任意两实数a,b,都可在同一数轴上找到其对应点A,B。若点A在点B右侧或A与B重合,则a≥b。 小于等于是一种判断方式,用来表示不等式左侧的值小于等于不等式右侧的值,符号为“≤”。例如3≤5。在各种数学,或编程中会出现。命题中,小于等于是小于或者等于,只要满足一个条件即可成立。小于等于又称为不大于。三、大小于符号的区分