一、根号2是多少 怎么算 要过程
√2= 1.4142135623731 ……
√2 是一个无理数，它不能表示成两个整数之比，是一个看上去毫无规律的无限不循环小数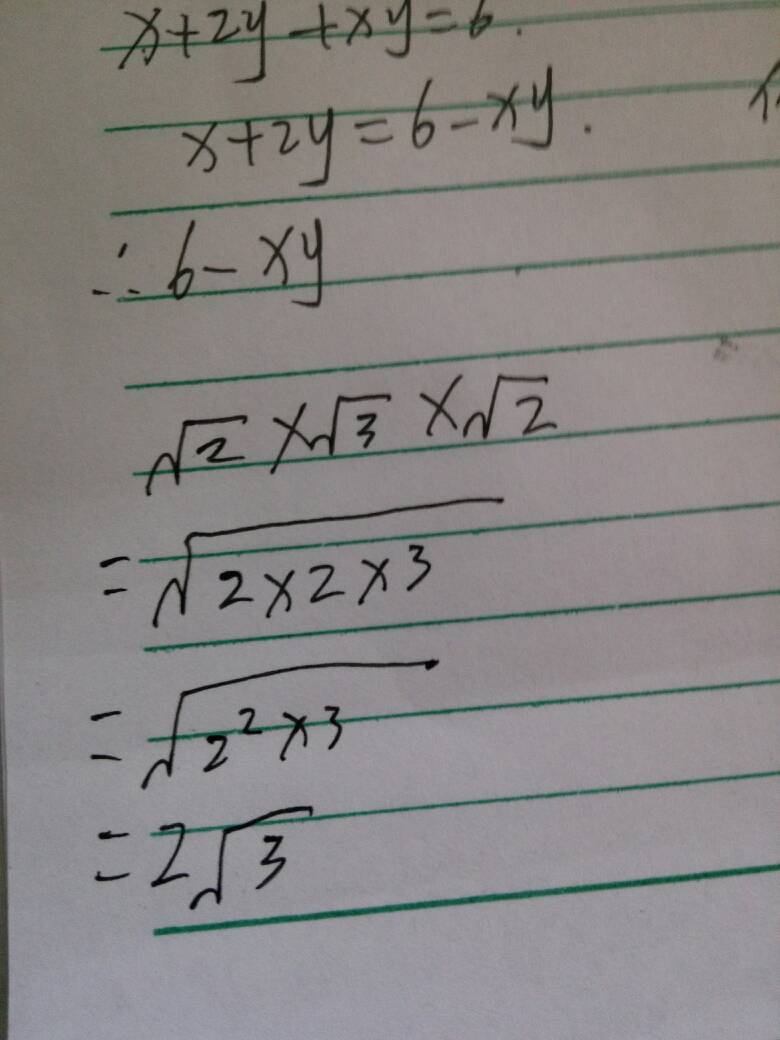
早在古希腊时代，人们就发现了这种奇怪的数，这推翻了古希腊数学中的基本假设，直接导致了第一次数学危机。
其实就是公式的逆运用（a+b)^2=a^2+2ab+b^2
例：1^2=1
(1+0.4)^2=1+0.8+0.04
(1.4+0.1)^2=1.96+0.028+0.0001
以此类推……
扩展资料：
常用的平方根：
√0 = 0（表示根号0等于0，下同）
√1 = 1
√2 = 1.4142135623731
√3 = 1.73205080756888
√4 = 2
√5 = 2.23606797749979
√6 = 2.44948974278318
√7 = 2.64575131106459
√8 = 2.82842712474619
√9 = 3
√10 = 3.16227766016838
√11 = 3.3166247903554
√12 = 3.46410161513775
二、根号二十等于多少
显然20=4*5
所以20不是完全平方数
根号20=2根号5
如果要得到近似值
使用计算器得到根号20约等于4.472
三、根号二到根号二十的值
根号二到根号二十的值如下：
扩展资料：
一个数的2次方根称为平方根；3次方根称为立方根。各次方根统称为方根。求一个指定的数的方根的运算称为开方。一个数有多少个方根，这个问题既与数的所在范围有关，也与方根的次数有关。
在实数范围内，任一实数的奇数次方根有且仅有一个，例如8的3次方根为2，-8的3次方根为-2 。
正实数的偶数次方根是两个互为相反数的数，例如16的4次方根为2和-2。
负实数不存在偶数次方根。
零的任何次方根都是零。
在复数范围内，无论n是奇数或偶数，任一个非零的复数的n次方根都有n个。
