驻点和拐点有什么区别?
区别:在驻点处的单调性可能改变,在拐点处单调性也可能发生改变,但凹凸性肯定改变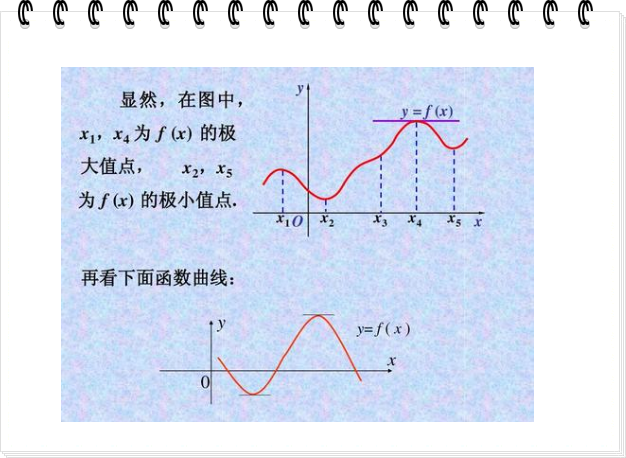
拐点不一定是驻点,例如y=x三次方+x。因为二阶导数某点为0不能判定一阶导数在某点为0。驻点显然更不一定是拐点,驻点只需要一阶导数为0,而拐点需要二阶可导。
扩展资料:
函数的导数为0的点称为函数的驻点,驻点可以划分函数的单调区间.(驻点也称为稳定点,临界点.)
在驻点处的单调性可能改变,在拐点处单调性也可能发生改变,但凹凸性肯定改变。
拐点:二阶导数为零,且三阶导不为零;
驻点:一阶导数为零。
二阶导数为零时,一阶不一定为零;一阶导数为零时,二阶不一定为零。
拐点与驻点的区别
拐点是函数的凹凸性发生改变的点。
驻点是使得函数的导数为0的点,是单调性“可能”发生变化的点。
可导函数的极值点一定是驻点,但驻点不一定是极值点,例如y=x^3,x=0是驻点,但不是极值点。
拓展资料:
拐点是导数符号发生变化的点。拐点点可以是相对最大值或相对最小值(也称为局部最小值和最大值)。如果函数是可微分的,那么拐点是一个固定点;然而并不是所有的固定点都是拐点。如果函数是两次可微分的,则不转动点的固定点是水平拐点。例如,函数 x ^ 3在x = 0处有一个固定点,也是拐点,但不是转折点。
在微积分,驻点(Stationary Point)又称为平稳点、稳定点或临界点(Critical Point)是函数的一阶导数为零,即在“这一点”,函数的输出值停止增加或减少。对于一维函数的图像,驻点的切线平行于x轴。对于二维函数的图像,驻点的切平面平行于xy平面。值得注意的是,一个函数的驻点不一定是这个函数的极值点(考虑到这一点左右一阶导数符号不改变的情况);反过来,在某设定区域内,一个函数的极值点也不一定是这个函数的驻点(考虑到边界条件),驻点(红色)与拐点(蓝色),这图像的驻点都是局部极大值或局部极小值。
驻点并不是点,而是和极值点相似,代表着这一点的x值。
因此,驻点不一定是极值点,极值点也不一定是驻点。