一、求末项、首项、项数的公式，急！！！！！！！！！
① 和=（首项+末项）×项数÷2
② 项数=（末项-首项）÷公差+1
③ 首项=2和÷项数-末项
④ 末项=2和÷项数-首项
(以上2项为第一个推论的转换)
⑤末项=首项+（项数-1）×公差
等差数列是指从第二项起，每一项与它的前一项的差等于同一个常数的一种数列，常用A、P表示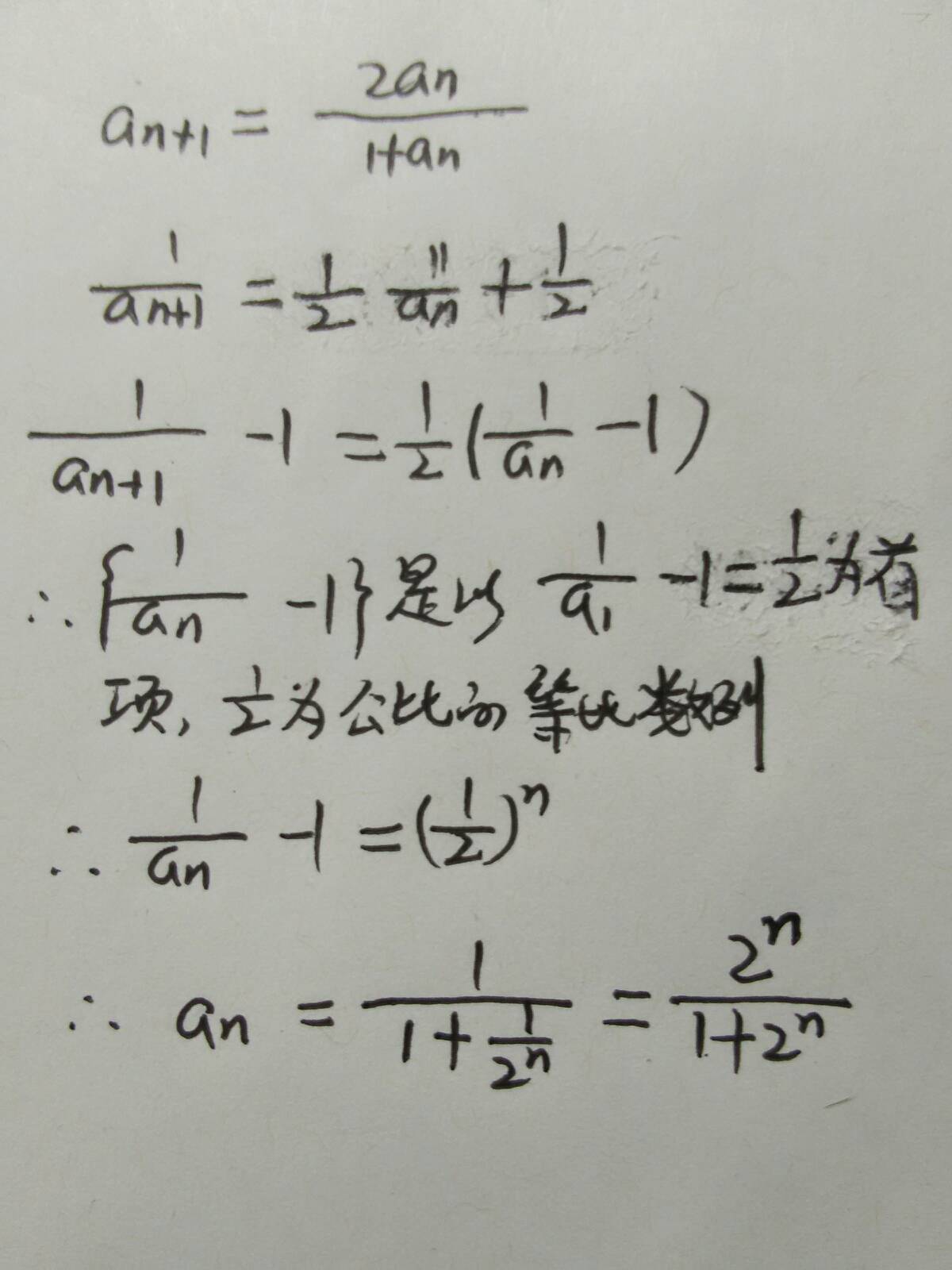
这个常数叫做等差数列的公差，公差常用字母d表示。
例如：1,3,5,7,9……2n-1。通项公式为：an=a1+(n-1)*d。首项a1=1，公差d=2。前n项和公式为：Sn=a1*n+[n*(n-1)*d]/2或Sn=[n*(a1+an)]/2。注意：以上n均属于正整数。
扩展资料：
从通项公式可以看出， 是n的一次函数(d≠0)或常数函数(d=0)， 排在一条直线上，由前n项和公式知， 是n的二次函数(d≠0)或一次函数 ，且常数项为0。
等差数列的判定：
（1） (d为常数、n ∈N*)或 ，n ∈N*，n ≥2，d是常数]等价于 成等差数列。
（2） 等价于 成等差数列。
（3） [k、b为常数,n∈N*]等价于 成等差数列。
（4） [A、B为常数，A不为0，n ∈N* ]等价于 为等差数列。
在有穷等差数列中，与首末两项距离相等的两项和相等。并且等于首末两项之和；特别的，若项数为奇数，还等于中间项的2倍,即， 中。
例：数列：1，3，5，7，9，11中 ，即在有穷等差数列中，与首末两项距离相等的两项和相等。并且等于首末两项之和。
数列：1，3，5，7，9中 。
即若项数为奇数，和等于中间项的2倍，另见，等差中项。
参考资料：百度百科——等差数列
二、数学项数公式是什么
①
和=（首项+末项）×项数÷2
② 项数=（末项-首项）÷公差+1
③
首项=2和÷项数-末项
④
末项=2和÷项数-首项
(以上2项为第一个推论的转换)
⑤末项=首项+（项数-1）×公差
三、项数公式是什么？
项数公式为：项数=[(尾数-首数)/公差]+1。
数列中项的总个数为数列的项数，项数是一个正整数。
无穷数列没有项数。
数列中项的总数之和为数列的“项数”，在数列中，项数是一个正整数。
项数在等差数列中的应用：和=（首项+末项）×项数÷2，项数=（末项-首项）÷公差+1，首项=2和÷项数-末项，末项=2和÷项数-首项(以上2项为第一个推论的转换)，末项=首项+（项数-1）×公差。
四、项数怎么求
求项数公式:项数=(末项-首项)÷公差+1。
数列中项的总数为数列的“项数”。数列（sequenceofnumber），是以正整数集（或它的有限子集）为定义域的函数，是一列有序的数。数列中的每一个数都叫做这个数列的项。
排在第一位的数称为这个数列的第1项（通常也叫做首项），排在第二位的数称为这个数列的第2项，以此类推，排在第n位的数称为这个数列的第n项，通常用an表示。
函数（function）的定义通常分为传统定义和近代定义，函数的两个定义本质是相同的，只是叙述概念的出发点不同，传统定义是从运动变化的观点出发，而近代定义是从集合、映射的观点出发。
函数的近代定义是给定一个数集A，假设其中的元素为x，对A中的元素x施加对应法则f，记作f（x），得到另一数集B，假设B中的元素为y，则y与x之间的等量关系可以用y=f（x）表示，函数概念含有三个要素：定义域A、值域B和对应法则f。其中核心是对应法则f，它是函数关系的。
五、如何求项数及项数的公式。谢谢！
项数公式:等差数列的项数=[(尾数-首数)/公差]+1。数列中项的总个数为数列的项数，项数是一个正整数。无穷数列没有项数。
数列中项的总数之和为数列的“项数”，在数列中，项数是一个正整数。
数列是以正整数集（或它的有限子集）为定义域的函数，是一列有序的数。数列中的每一个数都叫做这个数列的项。排在第一位的数称为这个数列的第1项（通常也叫做首项），排在第二位的数称为这个数列的第2项……排在第n位的数称为这个数列的第n项，通常用an表示。
项数在等差数列中的应用：
①和=（首项+末项）×项数÷2；
②项数=（末项-首项）÷公差+1；
③首项=2和÷项数-末项；
④末项=2和÷项数-首项(以上2项为第一个推论的转换)；
⑤末项=首项+（项数-1）×公差
相关公式：
末项＝首项+（项数-1）*公差
首项＝末项－（项数-1）*公差
项数＝（末项－首项）/公差+1
（1） 第20组中三个数的和？
通过观察得出每个括号中的三个数都成等差数列，把每个括号的数相加得出：
1+2+3=6
3+4+5=12
5+6+7=18
7+8+9=24
他们的和也成等差数列，则第20组中三个数的和为“以6为首项、6为公差、20为项数”的等差数列。
根据公式：末项＝首项+（项数-1）×公差
末项=6+（20-1）×6
=120
答：第20组中三个数的和是120。
（2）前20组中所有数的和？
前面讲过等差数列求和的算法，大家可以去看一下。
和=（首项+末项）×项数÷2
和=（6+120）×20÷2
和=1260
答：前20组中所有数的和是1260。
六、等比等差数列中的项数怎么算，有什么公式吗
有公式。等比数列项数公式：An=A1*q^（n－1）；等差数列项数公式：an=a1+(n-1)*d。
一、等差数列公式
1、举例等差数列：1、3、5、7、9；
2、首项：1；末项：9；公差：2；
3、等差数列求和：（首项+末项）*项数/2；
4、求项数：（末项-首项）/公差+1；
5、求首项：末项-公差*（项数-1）；
6、求末项：首项+公差*（项数-1）；
7、求公差：（末项-首项）/（项数-1）。
二、等比数列公式
1、等比数列的通项公式是：An=A1*q^（n－1）；
2、若通项公式变形为an=a1/q*q^n(n∈N*),当q＞0时，则可把an看作自变量n的函数，点(n,an)是曲线y=a1/q*q^x上的一群孤立的点；
3、n－1＝（an/a1）开n次根号；
4、n＝（an/a1）开n次根号+1。
扩展资料：
等差数列的判定
1、
(d为常数、n
∈N*)或
，n
∈N*，n
≥2，d是常数]等价于
成等差数列。
2、等价于
成等差数列。
3、[k、b为常数,n∈N*]等价于
成等差数列。
4、[A、B为常数，A不为0，n
∈N*
]等价于
为等差数列。
等比数列的判定
一个数列，如果任意的后一项与前一项的比值是同一个常数（这个常数通常用q来表示），且数列中任何项都不为0，即：这个数列叫等比数列，其中常数q
叫作公比。
参考资料：搜狗百科—等差数列
参考资料：搜狗百科—等比数列
